Sizing safety valves for supercritical steam boilers



helps to explain some of the above terms.
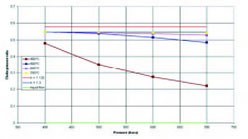
To calculate the choked flow condition for supercritical steam the Homogeneous Equilibrium Model is the reference method (Fisher 1992). It involves an isentropic expansion from an initial supercritical pressure and supercritical temperature. The mass flux (G) is calculated at each reduced pressure. The ss flux G goes through a maximum atm the choke pressure. This mass flux is the choke mass flux Gchoke. The vent area is then calculated. HEM can be evaluated using the Omega method developed by Leung (Leung 1996). The method involves a single isentropic expansion generally to 0.9 or 0.7 of the original pressure Po. The value of Omega is then calculated. There are also equations to calculate the choke pressure ratio, the choke pressure, the dimensionless mass flux and the choke mass flux. Forgas flow one can define a dimensionless mass flux Gchoke* similar to that used in the Omega method, but calculated using the isentropic coefficient. Values of k which were evaluated were k = 1.135 for saturated steam and k = 1.3 for superheated steam. Equations for choke pressure ratio and choke temperature ratio are also available.Example calculations were performed at four relieving pressures (400, 500, 600 & 700 bara) and four relieving temperatures (400, 500, 600 & 700°C). The required mass flow rate (Qm) was 20 000 kg/h. Isentropic expansion involves reducing the temperature (and pressure) whilst maintaining the same entropy - i.e. a vertical line downwards on the entropy – temperature diagram. Figures 2 shows the dimensionless mass flux (Gchoke*), obtained using the rigorous HEM, versus relieving pressure for a range of relieving temperatures. The figure also shows the dimensionless mass flux calculated using gas flow equations with two values of the isentropic coefficient (k) and calculated using a liquid flow equation. Figure 3 shows the critical pressure ratio (?c), obtained using the rigorous HEM, versus relieving pressure for a range of relieving temperatures. The figure also shows the critical pressure ratio calculated using gas flow equations with two values of the isentropic coefficient (k)
The results using HEM / Omega were:
For relieving temperatures of 500°C and above:
The chokes were in the superheated vapour region.
There was excellent agreement between HEM and Omega methods.
The value of Omega remains relatively constant during the isentropic expansion. For relieving temperatures of 400°C:
The chokes were in the sub-cooled liquid region.
There was less agreement between HEM and Omega methods.
The value of Omega varies considerably during the isentropic expansion.
If the chokes are in the superheated vapour region then the standard methods could also be evaluated. Accurate specific volume (v) was obtained from steam tables and was in good agreement with PPDS (PPDS 2004). There was excellent agreement between all gas flow methods using a particular k value in terms of calculated vent area. With k=1.3, the calculated flow areas were slightly higher than the reference methods.
With k = 1.135, the calculated flow areas were higher than reference methods but not unduly conservative. The recommended approach is to examine the relieving
pressure and relieving temperature:
If it lies above saturated vapour line, the choke is in the superheated vapour region. The rigorous HEM or Omega method can be used to determine the mass flux.
Reasonable predictions can be made for mass flux using the gas flow equations with k=1.3 and accurate specific volume data.
If it lies above the saturated liquid line, the choke is in the sub-cooled liquid region. The rigorous HEM is generally the only method able to predict mass flux. Use of a liquid flow equation may over-predict the mass flux and therefore under-predict the vent size needed.
If it lies directly above the critical point, or above the saturated vapour line but at a temperature below 500°C, it would be prudent to use the rigorous HEM. Further work is in progress to better define the applicability of different methods in the region.
Fisher HG et al "Emergency Relief System Design using DIERS technology" Chapter II, DIERS / AIChE, 1992. Leung "Easily Size Relief Devices and Piping for Two- Phase Flow" Chemical Engineeri g Progress, p28 December 1996. rvice (PPDS) for Windows, v3.1.4 TUV NEL Ltd, 2004. The full text of this paper appears in the 12th International Symposium, Loss Prevention in the Process Industries, Edinburgh, May 2007, IChemE Symposium Series No 153, Poster 08. Email contact: john.hare@hsl.gov.uk

| Telephone: | 0870 240 1978 |
| Email: | uksales@emerson.com |
| Website: | https://www.emerson.com/en-gb/automation/home |
| More information on the Emerson Process Management Ltd BVAA Member Directory Page |
Search related valve / actuator articles: Emerson Process Management LtdIssue 3Safety Valves











