Masterclass
Using Valves or Actuators in SIL Applications



An overview of what needs to be determined for the final element
To know what SIL capability is achievable from the final element, we need to know the probability of it being in the failed state when a demand for it to function occurs from the process. This is known as the average probability of failure on demand (PFDAVG). Ideally this is zero, but in reality, it will not achieve this and we therefore need to quantify its value from a probabilistic reliability model. The model must take into account the failure rates of all the constituent devices in the final element and its architectural integrity.
Because functional failures can also be systematic (non-probabilistic), we need to ensure the final element and its components have been designed with the appropriate systematic integrity, known as the Systematic Capability (SC 1, 2, 3 or 4). (The SC number of the final element must at least match the SIL number of the application).
So, this means the following measures need to be determined for the final element in relation to its specified function:
1. the average probability of failure on demand (PFDAVG)
2. the architectural integrity (see BS EN 61508 requirements below for more details)
3. the systematic capability (SC 1, 2, 3 or 4)
Any of the three measures above can place a limit on the SIL so each needs to be determined independently.
Key requirements from BS EN 61508 and/or BS EN 61511
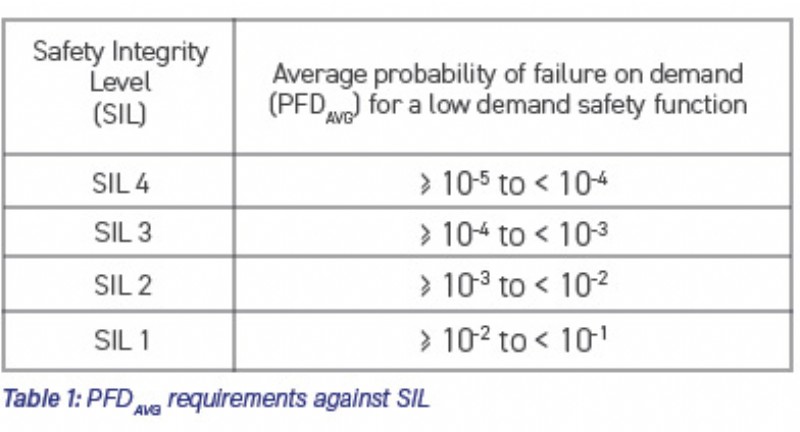
Most safety instrumented functions (SIFs) in the process industry are ‘low demand’. This means the likelihood of them getting a demand to put the plant into a safe state is assessed to be low (several other independent protection measures would all have to fail before a SIF demand occurs). The PFDAVG of a low demand safety instrumented function (SIF) required to achieve a SIL, given in BS EN 61508 and BS EN 61511, is as follows:
The PFDAVG for the SIF is the sum of the PFDAVG values for each subsystem. The division of the system PFDAVG into the three percentages shown in Figure 1 is not in the standards but seems to be generally accepted in industry as reasonable targets for the subsystem vendors. (Note, some specifiers have occasionally been known to use values >50% for the final element).
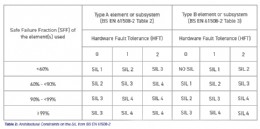
Each subsystem may be formed from redundant elements to increase architectural integrity. This often leads to an increased “SIL capability” (i.e., SIL limit) of a subsystem. BS EN 61508-2 sets limits on the maximum SIL that a subsystem can claim, known as the Architectural Constraints (from BS EN 61508-2 Tables 2 and 3). This limit is determined by the ‘hardware fault tolerance’ (HFT) within the subsystem (i.e., the redundancy of elements), the ‘safe failure fraction’ (SFF) of the individual element(s) and whether the elements used are of simple technology (‘type A’) or more complex technology (‘type B’) in terms of their known failure modes.
Mechanical (or electro-mechanical) elements would generally be considered as being of type A. The SFF is the proportion of failures in an element that are ‘safe’ (plus those that would be rendered safe by any diagnostics), divided by the safe and dangerous failures. (‘Safe’ failures generally result in a spurious trip, whereas ‘dangerous’ failures cause the SIF to be unavailable). If there are no diagnostics, SFF reduces to λS / (λS + λD).
Architectural constraints only apply to subsystems and elements (not systems); the SILs in Table 2 above impose a SIL limit on the SIF in which the subsystem is used (unless further architectural measures are used).
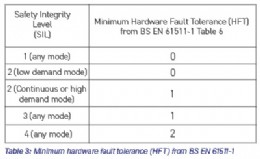
SIS designers in the process industry will normally be working to BS EN 61511-1. This standard offers alternative requirements for the architectural integrity that does not require meeting a SFF or type (A/B) definition, but instead stipulates a minimum HFT depending on the SIL and the demand mode of the SIF, as shown below:
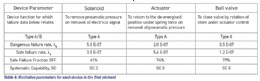
A worked example of a final element reliability model To illustrate a simple reliability model, we shall take the example of a final element formed by a single solenoid, pneumatic actuator and ball valve. We’ll assume the SIL related parameters for these proposed devices are available from the manufacturer (e.g., in their respective safety manuals).
These are summarised in Table 4 below. Note, the values shown are only for illustration – they are not based on real element data so don’t use them in a real project! (Refer to Part 2 of this series where the device parameters were explained). To keep things simple for this article we shall assume there are no external diagnostics used on the final element.
For this example, we shall define the required function of the final element as: To close the ball valve on de-energisation of the solenoid, and that the SIF (which is performed by the sensor, logic and final element) is required to meet SIL 2.
Typically, a device manufacturer will classify failure modes of the device as ‘dangerous’ (λD), ‘safe’ (λS), etc, but these terms are only meaningful with respect to the target SIF application. Manufacturers of mass produced devices can only assume a general context of use if they are making these classifications, at best. It is therefore essential that the final element designer only uses vendor failure data if it fits with the specific SIF application, otherwise the model is invalid and gross numerical errors can result.
Part of this suitability check for the target application considers whether each device performs its function by de-energisation (e.g., by force of the actuator return spring) or by energisation (e.g., relies on the availability of a utility supply).
Reliability modelling
A common modelling method is a Reliability Block Diagram (RBD) which represents the series and parallel paths of reliability. (This representation also shows the HFT visually). This will indicate which equations to use in calculating the PFDAVG. The blocks represent each device and can be attributed with the respective failure data. Where the diagram for the subsystem architecture indicates the blocks are in series their failure rate figures of the same type can be summed, and likewise for each of the other λ-figures, giving series-summed totals for λDD, λDU, and λS. Where blocks are in parallel the equations from BS EN 61508-6 for common redundant architectures can be used. This is illustrated in Figure 2 for a proposed simplex channel implementation of the SIF (using the BS EN 61508-2 requirements for architectural integrity).
Note that because in this case there are no diagnostics in/for any elements, λDD is zero and λDU is effectively = λD. For the same reason, the diagnostic coverage (DC) is zero and the safe failure fraction (SFF) reduces to λS / (λS + λD).
The analysis and results in Figure 2 can be compared with the requirements from BS EN 61508-2 in Tables 1 and 2 above. It can be seen that the overall capability of the final element is limited to SIL 1 due to the Architectural Constraints of the solenoid being the “weakest link”. (The PFDAVG and SC would otherwise indicate SIL 2).
So, the requirements of SIL 2 for the SIF will not be met with the implementation shown in Figure 2. Addressing the “weakest link” leads to the proposal in Figure 3 where the Architectural Constraints of the solenoid has been increased by adding a second solenoid (i.e., giving an HFT of 1 for this element).
By comparing the results of this implementation against the requirements of BS EN 61508-2 in Tables 1 and 2 above shows that a SIL 2 capability is now achieved for the final element package for its use in the specified SIF.
Note that the systematic capability (SC) cannot be modelled as it is not a probabilistic quantity. It is just shown for information alongside the probabilistic parameters so it can be considered in the “weakest link” evaluation.
Explanation of some terms used in the PFD calculation Looking at the equations used for the calculation of PFDAVG it can be seen that certain terms are used that need to be defined. These are as follows:
T1 The ‘proof test interval’ – the time in hours between full (in-situ) tests of the SIF
MTTR The ‘mean time to restoration’ – the time allowed to complete any repairs that have been found necessary as a result of proof tests (or any diagnostics if used)
β This factor is to account for the probability that multipledevices in a parallel (redundant) configuration may fail due to a common cause. The β-factor is a proportion of the λD value for each device in the parallel combination. There are methods to determine β based on considerations such as diversity of device manufacturer, complexity or technology used in the devices, environment, physical proximity to each other, etc. Values for β typically fall into the 3-5% region using these methods so for simplicity and conservatism we have used 10% in this example.
Can the SIL capability be increased any further? Sometimes, as in the example of Figure 2, the analysis does not initially yield the SIL capability that is required. In this case it may be possible to increase SIL capability by one or more of the following methods depending on whether the PFDAVG or Architectural Constraints is the limiting issue:
• Reduce the proof test interval (T1) which will decrease the PFDAVG
• Increase the hardware fault tolerance HFT
• Provide external diagnostics (which may improve PFDAVG and Architectural Constraints depending on the diagnostic test interval, process safety time of the application and change in ‘type A/B’)
• Apply partial valve stroke testing which will decrease the PFDAVG
If the plant operator uses higher values for T1 and MTTR than those used in the reliability analysis, then the PFDAVG needs to be recalculated to ensure it still meets the required SIL.
If the plant operator cannot use either of the first two options above, the last two options can be considered, but these get quite a bit more complicated - maybe a subject for another article in the future!
Tel: 01244 457 671
Email: paul.reeve@silmetric.com
Web: www.silmetric.com

| Telephone: | 01244 457671 |
| Email: | infor@silmetric.com |
| Website: | www.silmetric.com |
| More information on the Silmetric Ltd BVAA Member Directory Page |
Search related articles: Silmetric LtdIssue 45Safety and StandardsSILsStandardsMaster ClassTraining














